《算法图解》读书笔记6-图以及广度优先搜索
algorithms Linux什么是图
图模拟一组链接,图由顶点和边组成。一个顶点可能与众多顶点直接相连,这些顶点被称为邻居。
图通常表示为:G(V,E),其中,G表示一个图,V是图中顶点的集合,E是图中边的集合。
简单图
在图结构中,若不存在顶点到其自身的边,且同一条边不重复出现,则这样的图称之为简单图。
无向图
如果图中任意两个顶点之间的边都是无向边,则称该图为无向图。
无向边:若顶点 M 到顶点 N 的边没有方向,称这条边为无向边,用无序偶对(M,N)或(N,M)表示。
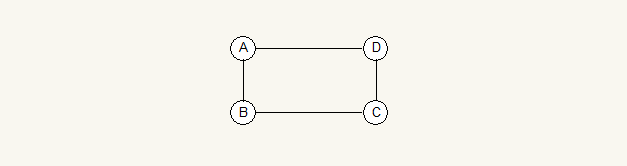
无向图是有边和顶点构成。如下图所示就是一个无向图 G1:
无向图G1= (V1,{E1}),其中顶点集合 V1={A,B,C,D};边集合E1={(A,B),(B,C),(C,D),(D,A)}
有向图
如果图中任意两个顶点之间的边都是有向边,则称该图为有向图。
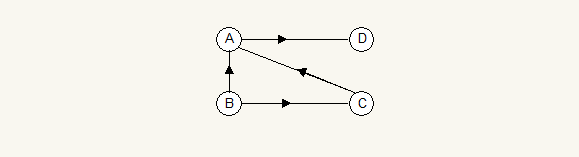
有向边:若顶点 M 到顶点 N 的边有方向,称这条边为有向边,也称为弧,用偶序对 < M, N >表示;M 表示弧尾,N 表示弧头 有向图是有弧和顶点构成,如下图所示是一个有向图 G2:
有向图 G2=(V2,{E2}),其中顶点集合 V2={A,B,C,D};弧集合 E2={< A,D>,< B,A>,< C,A>,< B,C>} 对于弧< A,D>来说, A 是弧尾,D 是弧头 注意:无向边用 小括号 “()”表示,有向边用“<>”表示。
更多相关资料:请访问参考链接 1
广度优先搜索(BFS—breadth first search)
广度优先搜索可以回答两类问题:
- 第一类问题:从节点 A 出发,有前往节点 B 的路径吗?
- 第二类问题:从节点 A 出发,前往节点 B 的哪条路径最短?
在解决广度优先搜索问题时,需要按照一定的顺序进行搜索,不能跨顶点。这时候需要用到一种数据结构——队列。
队列
队列的工作原理与现实生活中队列完全相同。好比排队买票,排在前面的就先买到票。队列中的数据也是这样,先加入到队列中的元素,会被优先取出,不能随机的访问队列中的元素。队列只支持两种操作:入队 和 出队。
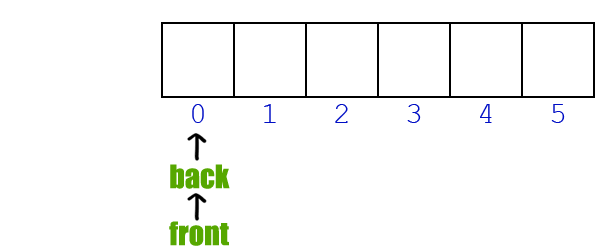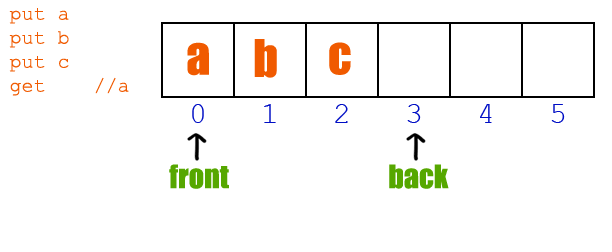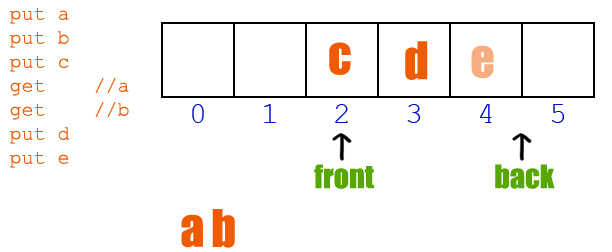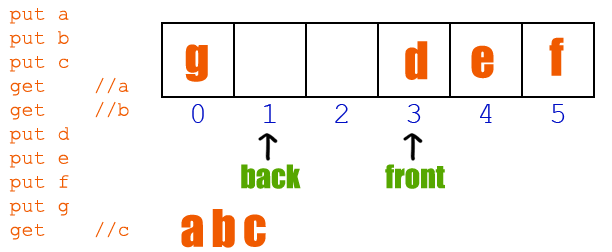
队列是一种先进先出 (First In First Out, FIFO)的数据结构。队列是有长度的,在定义的时候设定好后,内存就申请好了。队列在内存中的操作流程如下如所示:
常常与队列做比较学习的是栈,栈是一种后进先出(Last In First Out, LIFO)的数据结构。
BFS 实现
摘录书中以苹果经销商的例子阐述了广度优先搜索算法的简单实现。
#coding:utf-8
from collections import deque
#用散列表实现图
graph = {}
graph["you"] = ["alice", "bob", "claire"]
graph["alice"] = ["peggy"]
graph["bob"] = ["anuj", "peggy"]
graph["claire"] = ["thom", "jonny"]
graph["peggy"] = []
graph["anuj"] = []
graph["thom"] = []
graph["jonny"] = []
# 搜索朋友里面谁是 seller
def search(name):
#创建搜索队列
search_queue = deque()
#初始化搜索队列
search_queue += graph[name]
#记录已经搜索过的人
searched = []
#只要队列不空就一直搜索
while len(search_queue) > 0:
#取出队列中最先加进去的一个人
person = search_queue.popleft()
# 只有他没有被搜索过才进行搜索
if not person in searched:
# 查看是不是seller
if person_is_seller(person):
print(person + " is a seller")
return True
else:
# 不是seller,所以将他的朋友都加入搜索队列
search_queue += graph[person]
# 标记这个人已经被搜索过了
searched.append(person)
return False
# 判定是不是seller,规则是名字以 m 结尾就是 Seller
def person_is_seller(person):
if person[-1] == "m":
return True
else:
return False
# 测试
search("you")